Introducing tolls

and my substack

1. Introduction

Welcome to Critical Density, a substack about transportation economics. I am assistant professor of civil engineering at University of Illinois Urbana-Champaign The point of the substack is to explain theoretical ideas and how they relate to real issues.

By way of introduction I will talk about how people respond to the introduction of tolls on roads that were free. This is topical, because on Sunday January 5th New York City will launch a system of tolls in or out the pictured area.

2. Large elasticity at introduction

New York will be the sixth major city (alongside Singapore, London, Stockholm, Milan and Gothenburg) with downtown congestion pricing: i.e., charging tolls on driving into downtown areas to curb congestion. I wrote a paper on the history of downtown congestion pricing and noticed a pattern:

1. Tolls were introduced, and driving fell much more than forecast.

2. Tolls were later on raised, and driving fell much less than forecast.

These are entries into London’s Congestion Charging Zone. See if you can guess when the charge was introduced and when it was increased.

https://content.tfl.gov.uk/central-london-congestion-charging-impacts-monitoring-sixth-annual-report.pdf

The pattern played out in a particular way. Ordinarily, forecasts assume people react to different costs of driving equally—including tolls, gasoline, parking, etc. These add up to a “money cost” measure. Define these symbols:

\(\begin{align} t &&\text{toll} \\ m_0 & & \text{parking, gas, etc.}\\ m & = m_0 + t & \text{full money cost of a trip} \\ D(m) & & \text{demand function} \end{align}\)

Forecasters estimate a demand function D(m) that gives the number of trips into a downtown for a given money cost. So a demand function treats a $5 increase in parking cost as equivalent to introducing a $5 toll. The elasticity of demand with respect to money cost, evaluated at some money cost m is:

\(\varepsilon(m) = \frac{D'(m) m}{D(m)}\)

What I noticed is that the elasticity of demand with respect to money cost was larger when tolls were introduced than when they were later increased. In my paper “Large Elasticity at Introduction,” I name this phenomenon Large Elasticity at Introduction (LEI). Here are numbers from Sweden:

Transport for London (2008):

the elasticity in response to the introduction of the £5 charge, at −0.55, was much higher than that of −0.16 in response to the increase in the charge from £5 to £8.

Olszewski and Xie (2002, p. 227) on Singapore:

The first introduction of road pricing in the form of ALS [Area License Scheme] in 1975 had the most dramatic effect on traffic volumes and showed the highest [sic largest] elasticity which was never observed again.

There are no numbers from a toll increase in Milan as far as I know.

4. Large Elasticity at Introduction is not obvious

Sometimes people say LEI is obvious: “Oh the initial charge tolls off the most elastic traffic, leaving only the inelastic travelers.” But in what sense are the people who quit driving the most elastic? In the sense that they quit driving when you charge them a toll. This is the dormitive principle that Paul Krugman has complained about (p. 8).

Some people think I mean that the toll moves demand to a “flatter” part of the demand curve (or “steeper” if they’re talking about an inverse demand curve). But you can’t tell an elasticity by looking at a curve. Here is exp(-m). It gets flatter as m rises but its elasticity increases.

Here are three common functional forms for demand (where α is the maximum possible demand and β indexes how sensitive demand is to money). Take their elasticities and then differentiate elasticity with respect to money cost m:

\(\small \begin{align} \textrm{logit:} \quad D(m) &= \frac{\alpha}{1+e^{\beta m}} &\varepsilon(m) & = -\beta m (1-D/\alpha) & \varepsilon'(m) &= -\beta (1-D/\alpha) (1+\beta m D/\alpha)\\ \textrm{exponential: } \quad D(m) & = \alpha/e^{\beta m} &\varepsilon(m) &= -\beta m & \varepsilon'(m) &= -\beta \\ \textrm{linear:} \quad D(m) & = \alpha - \beta m & \varepsilon(m) &= -\beta m/D & \varepsilon'(m) &= -\alpha \beta/D^2 \end{align}\)

The last column shows the change in elasticity with respect to money cost. They’re negative, so all the elasticities get more negative (i.e., larger in magnitude) as money cost grows. In other words, these demand functions would show the opposite of LEI: elasticity larger at the toll increase than at introduction.

Demand functions will often exhibit reverse-LEI because of what demand functions are supposed to be. Let v be the most someone would pay for a trip into the tolled area. Let F(v) be the cumulative distribution of v among potential travelers. The demand function D(m) should be proportionate to 1-F(v=m): i.e., the observed demand should be proportionate to the fraction of people who would pay at least m for a trip. If F is from any distribution you’ve probably ever heard about, then the elasticity of 1-F(m) grows (gets more negative) as m rises (e.g., logistic, normal, extreme value, Laplace, chi, chi-squared, uniform, exponential, Weibull, gamma, inverse Gaussian, Student’s t, F and many more).

5. What is going on

I believe LEI happens because some people just won’t pay a toll. So we could do this:

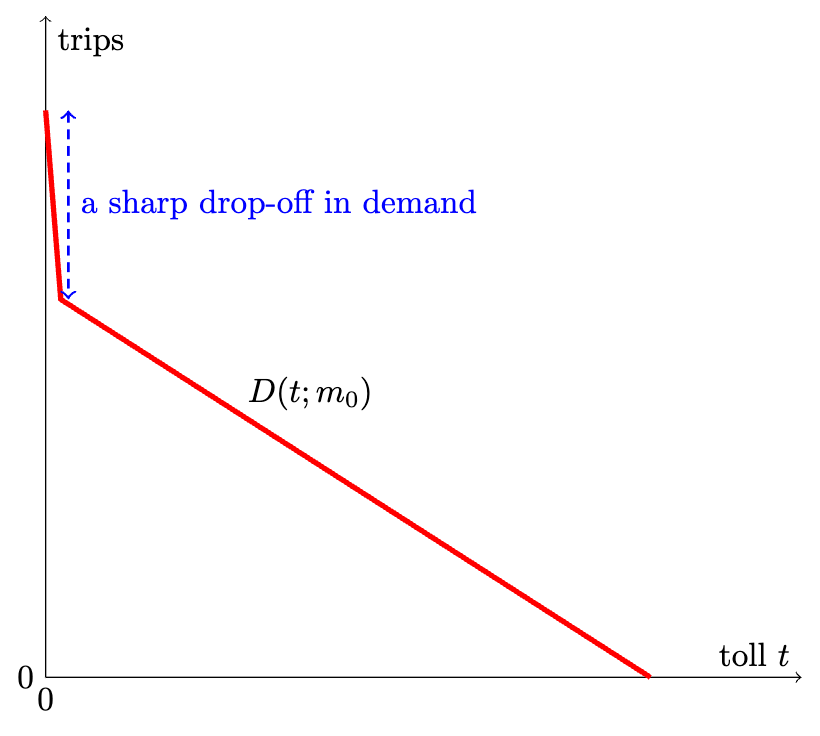
1. Write the demand function as a function of the toll, D(t).

2. Give D(t) a drop at zero.

The demand function will then look something like this:

demand discontinuity at zero

I call this DDZ: demand discontinuity at zero. DDZ produces LEI. Is there a literally vertical drop at zero? That would mean charging like one cent would repel a substantive amount of traffic. There’s no way to know for sure. What I think is that, for all practical purposes, we can act as if it is vertical at zero. Since one-cent tolls are not on the table, if we act as though the function is vertical at zero then we will not make different decisions than if it is actually shaped like this:

a sharp drop-off in demand

6. DDZ is consistent with other facts

A DDZ for tolls is consistent with other things we see.

Bus agencies that nix fares see sharp increases in demand, while those that add fares see sharp drops in demand. A review, Volinski (p. 13, 2011), notes that elasticities calculated from bus fare changes are way smaller than those from eliminating or adding fares. Ridership on the Atlanta Streetcar fell 58 percent when they imposed a $1 fare.

In a review of parking pricing, Marsden (2006) notes:

The evidence does suggest however that some commuters are prepared to walk substantially further than previously considered to take advantage of free parking….The reported evidence on willingness to walk to take advantage of free parking spaces is surprising given the identification of the importance of out-of-vehicle costs in the mode-choice decision.

So if you estimate some model to predict how far people will walk to save money on parking, and you calibrate it with choices made among different (non-zero) levels of parking prices, then you will dramatically underestimate how far they will walk for free parking.

In 2017, Stockholm introduced parking charges on suburban residential parking and increased pre-existing charges for downtown parking. Nissan et al., (2020) find:

We find a 35-40 percent reduction in the number of parked cars in response to the introduction of parking fees in the suburbs. However, the increase in the parking fees in the inner city had a substantially lower effect or no effect at all on demand.

A DDZ appears in many public health studies reviewed by JPAL: e.g.,

take-up of insecticide-treated bednets among pregnant women at antenatal care clinics in Kenya dropped by 60 percentage points (from 99 percent to 39 percent) when the price increased from zero to US$0.60—an amount that still represented a 92 percent subsidy of the US$7 market price.

Note here the result is not “people won’t pay for bednets.” It’s that going from $0 to $0.60 produces a much more massive drop than going from $0.60 to some other price.

7. Why is there a DDZ?

Here are two candidate explanations.

First, a psychological phenomenon called the zero price effect. Land Transport Authority Officials have pointed to the zero price effect to explain the phenomenal drop in traffic from the introduction of congestion pricing in Singapore. It also makes sense as an explanation for why things like a small tax on plastic bags reduces usage so much.

Second, transaction costs: any hassles involved in payment. I believe this is the most important factor, though I mean “hassles” in a broad sense. For example, in 2010 carpools started having to pay $2 tolls to cross the Bay Bridge, and carpooling dropped a lot. Why?

Focus groups with carpoolers indicated that the presence of a toll, and not just the dollar amount of it, contributed to the drop in carpoolers. Casual carpoolers were confronted for the first time whether and how to share costs. The social dynamics this set into motion were uncomfortable for many, and some decided not to continue the practice. —Deakin et al., (2012)

So some people changed behavior in a way that substantially affected their lives, because it was awkward to talk about how to split $2. I can relate, as someone who will usually just eat the french fries rather than bring up that I ordered onion rings.

Hodge, Orrell and Straus (1994) have noted the same about bus fares:

Of particular importance is how ridership increases associated with fare-free policies can largely be explained by a significant drop in the psychological costs associated with the fare box. The removal of the farebox can eliminate a barrer in the minds of potential passengers, many of whom may see the fare box as a source of confusion and potential embarrassment.

8. Some lessons for practice

8.1 The choice of toll level is mainly about how much money you raise

If what I’m saying is true, then a small toll will have a pretty similar effect on externalities (traffic, noise, pollution) as a substantially larger toll—or at least more similar than people expect.

Likewise, even though a dynamic toll that changes by time of day is better than a flat toll, it’s not that much better. For example, the Stockholm Congestion Tax is much lower in the middle of the day than during the peaks, so forecasts at the introduction expected demand to fall less during the off-peaks. In fact traffic fell by similar amounts in the peak and off-peak, so the forecasts underestimated the fall in off-peak traffic, as shown below:

from Eliasson et al., (2013) Accuracy of congestion pricing forecasts

It follows that the question of how much to charge matters a great deal to revenues but not as much to traffic and its externalities. For externalities the big question is whether you charge. I believe this is especially true of pollution. Here is a figure from Barth and Boriboonsomsin (2008) that shows emissions per mile about 2-3x as high at 5 mph as at 20 mph. So if tolling reduces the number of cars per day that head into a downtown area, then you don’t just get the effect of “fewer trips” but also substantially “less emissions from each trip.” In turn, traffic speed is also convex to flows, so we have convexity piled on convexity. So the drop in demand from introducing a small toll will pack a punch.

8.2 Watch out for free alternatives

Recall that the parking literature suggests “some commuters are prepared to walk substantially further than previously considered to take advantage of free parking.” Likewise, some people will reroute their trips in a way that wastes substantial time in order to avoid tolls. That can be alright but it’s something to keep an eye on.

Here is a cautionary tale. Traffic has been way below forecast on the tolled Ohio River Bridges in Louisville ($2.61 if you have a transponder) because people keep diverting to an old, free bridge (the Clark Memorial/US 31) . That free bridge is now deteriorating and more dangerous. In retrospect it was probably bad to encourage people to use the free bridge: the Environmental Justice mitigation for tolling included “Construct a Direct Free-Flow Connection between Non-Tolled US 31 Clark Memorial Bridge and I-65” and “Deploy signs along travel corridors through EJ [Environmental Justice] areas identifying access to the non-tolled US 31 George Rogers Clark Memorial Bridge and the I-64 Sherman Minton Bridge.” See City Observatory’s articles about the Ohio River Bridges project.

Crashes on the untolled Clark Memorial Bridge source: WDRB https://www.wdrb.com/in-depth/truck-crashes-are-increasing-on-the-clark-memorial-bridge-should-big-rigs-be-banned/article_517659b0-0bcd-11ef-b466-5b6fdd6216eb.html

8.3 Exemptions are consequential

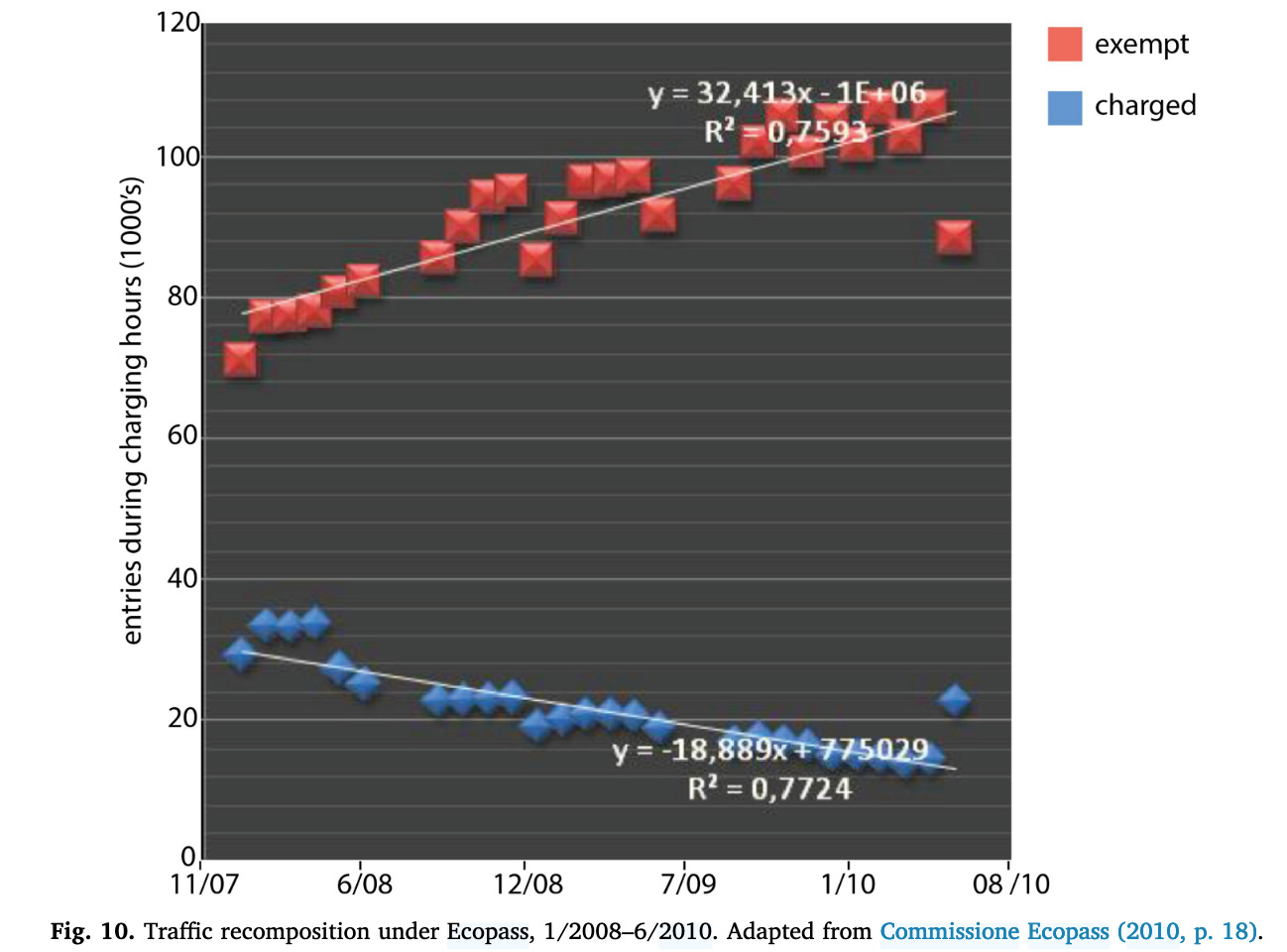
A motif I noticed in my history of downtown congestion pricing is that governments retract their toll exemptions because people use them more than expected. This makes sense if you think some people will change their behavior a lot to avoid a toll. When Singapore imposed its License Scheme, solo trips into the Restricted Zone immediately fell over 70% and the share of (exempt) carpool trips jumped from 8% to 37% immediately and eventually peaked at 54% when they eliminated the exemption. Here is a graph from Milan’s Ecopass system which had many exemptions.

Fortunately, New York’s tolls won’t have as many exemptions as I’d initially feared—especially since they aren’t relying on license plates for the disability exemption.

Thank you for reading

Next I’ll write about (i) taxes on ridehailing and (ii) whether congestion pricing can actually increase traffic flow.